|
Multilateration, also known as hyperbolic positioning, is the process of locating an object by accurately computing the time difference of arrival (TDOA) of a signal emitted from the object to three or more receivers. It also refers to the case of locating a receiver by measuring the TDOA of a signal transmitted from three or more synchronised transmitters.
Multilateration should not be confused with trilateration, which uses absolute measurements of time-of-arrival from three or more sites.
Principle
Multilateration is commonly used in civil and military surveillance applications to accurately locate an aircraft, vehicle or stationary emitter by measuring the time difference of arrival (TDOA) of a signal from the emitter at three or more receiver sites.
If a pulse is emitted from a platform, it will arrive at slightly different times at two spatially separated receiver sites, the TDOA being due to the different distances of each receiver from the platform. In fact, for given locations of the two receivers, a whole series of emitter locations would give the same measurement of TDOA. Given two receiver locations and a known TDOA, the locus of possible emitter locations is a hyperboloid (a surface approximately shaped like two cones joined at the points). In simple terms, with two receivers at known locations, an emitter can be located onto a hyperboloid. Note that the receivers do not need to know the absolute time at which the pulse was transmitted - only the time difference is needed.
Consider now a third receiver at a third location. This would provide a second TDOA measurement and hence locate the emitter on a second hyperboloid. The intersection of these two hyperboloids describes a curve on which the emitter lies.
If a fourth receiver is now introduced, a third TDOA measurement is available and the intersection of the resulting third hyperboloid with the curve already found with the other three receivers defines a unique point in space. The emitter's location is therefore fully determined in 3D.
In practice, errors in the measurement of the time of arrival of pulses mean that enhanced accuracy can be obtained with more than four receivers. In general, N receivers provide N-1 hyperboloids. When there are N > 4 receivers, the N-1 hyperboloids should, assuming a perfect model and measurements, intersect on a single point. In reality, the surfaces rarely intersect, because of various errors. In this case, the location problem can be posed as an optimization problem and solved using, for example, a least squares method or an extended Kalman filter.
Additionally, the TDOA of multiple transmitted pulses from the emitter can be averaged to improve accuracy.
Reciprocal case: locating a receiver from multiple transmitter sites
Multilateration can also be used by a single receiver to locate itself, by measuring the TDOA of signals emitted from three or more synchronised transmitters at known locations. This can be used by navigation systems, an example being the World War II British DECCA navigation system, which used the phase-difference of two transmitters, rather than the TDOA of a pulse, to define the hyperboloids. This allowed the transmitters to broadcast a continuous wave signal. Phase-difference and time-difference can be considered the same for narrow-band transmitters.
Derivation
Consider an emitter at unknown location (x,y,z) which we wish to locate. Consider also a multilateration system comprising four receiver sites at known locations: a central site, C, a left site, L, a right site, R and a fourth site, Q.
The distances from the left, right and Qth side sites to the central site are defined as follows:
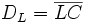 -
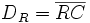 -
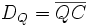
Then the time difference of arrival between pulses arriving directly at the central site and those coming via the side sites can be shown by basic time relations to be:
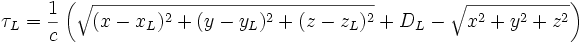 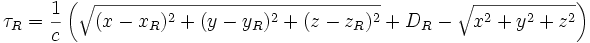 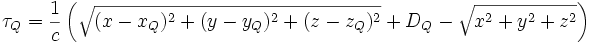
where 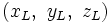 is the location of the left receiver site, etc, and is the location of the left receiver site, etc, and  is the speed of propagation of the pulse, often the speed of light. Each equation defines a separate hyperboloid. is the speed of propagation of the pulse, often the speed of light. Each equation defines a separate hyperboloid.
The multilateration system must then solve for the unknown target location (x,y,z) in real time. All the other symbols are known.
Note that in civilian air traffic control multilateration systems, the unknown height, z, is often directly derived from the Mode C SSR transponder return. In this case, only three sites are required for a 3D solution.
Multilateration accuracy
Multilateration is, in general, far more accurate for locating an object than techniques such as triangulation (as it is easier to measure time accurately than it is to form a very narrow beam). The accuracy of multilateration is a function of several variables, including:
- The geometry of the receiver(s) and transmitter(s)
- The timing accuracy of the receiver system
- The accuracy of the synchronisation of the transmitting sites or receiving sites. This can be degraded by unknown propagation effects.
- The bandwidth of the emitted pulse(s)
- Uncertainties in the locations of the receivers
Example applications
- Decca Navigator System - A system used from the end of World War II to the year 2000, employing the phase-difference of multiple transmitters to locate on the intersection of hyperboloids
- GEE - British aircraft location technique from World War II, using accurate reference transmitters
- Loran C - navigation system using multiple synchronised transmitters
- Passive ESM multilateration systems, including Kopáč, Ramona, Tamara, VERA and possibly Kolchuga - location of a transmitter using multiple receivers
- GSM localization - using multiple base stations to estimate phone location (by either the phone itself, or the phone network)
See also
External links
|


